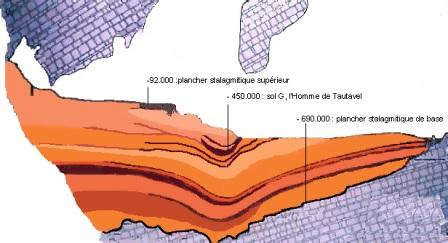
Currently, the geology is represented by some sparse stratigraphy slices that are manually drawn on paper sheets. These data should be digitized, interpolated and combined in order to obtain a continuous 3D digital model of the subsoil of the excavation site. Moreover, new devices which are available on the market, allow to obtain directly digital data of the walls or the floor of an excavation site by laser scanning or photogrammetry. Such data could be integrated with the subsoil model in order to build a global 3D digital model of the excavation site. This implies to fuse 3D models based on the stratigraphic slices with 2,5D or 3D models obtained by photogrammetry or laser scanning. Thus, the mathematical structure of the models must be multidimensional to be adaptable to all the topologies, in particular, in order to manage the holes.
The other requirement is to be able to deform, if possible in real-time, the 3D model. This will allow the user to refine the geometry of the model in order to correct some inaccuracies in data acquisition. Moreover, if a physical model can be associated to the geometry model, the user will be able to study the geological dynamics and simulate the deformation of the layers since the burying of the fossils.
To deal with these two requirements, we propose to use 2D and 3D deformable models. A deformable model is a mathematical model (curve, surface or volume), defined by parameters or a list of discrete points, which position is computed by minimizing an energy defined by the distance to reference data and by some constraints set by the user. It is then possible to make this model deform in order that it fits the data, while being under the interactive control of the user and keeping a reference shape or following some mathematical properties. More precisely, we intend to use the simplex meshes developed by Hervé Delingette, Director of Research, EPIDAURE Project, INRIA Sophia Antipolis, France. It is possible to integrate 1D, 2D and 3D simplex meshes in the same framework and to define, for each dimension, consistent fusion and cutting operators. These discrete meshes can model structures of all topologies and are defined by a simple mathematical formula which is fast to evaluate. Moreover, it is easy to introduce specific mathematical constraints. In particular, it will be possible to associate to the different geological layers modelled by 3D meshes, a physical behavior according for example to some Soil Mechanics results.